N-queen problem

Here is the solution for N-queen problem. N-queen problem is the classic example of backtracking algorithm. The problem statement is as follows :-
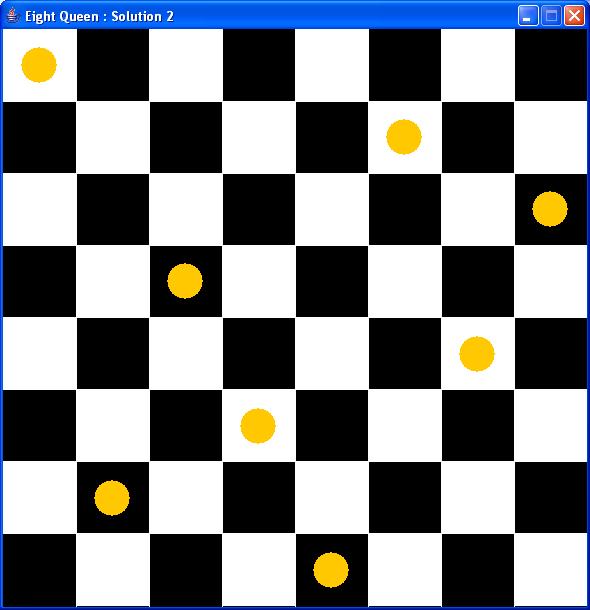
Given an N*N chessboard, place N queens on the chessboard such that no queen is attacking any other queen.
e.g. Here is a one such arrangement for N=8.





This is how the problem is solved using c program.
We will have an array of n integers say Chess[N]. Now Chess[i] saves the column position of a queen which is in row i. We start with Chess[0] =0, i.e. by considering zeroth position for queen in row zero. Next we consider position of queen in column 1. We will start by putting values of Chess[1] from 0 and check if it is proper position. If it is not proper position we will increment Chess[1] by 1 and check again. Continue this till we get proper position for Chess[1]. Next we will move to Chess[2] and so on. At any time we will have to check position of ith row only with respect to 0 to i-1th row.

In the program instead of array we have used the String of length N. The ith character denotes the position of queen in row i. With this the only changes we need from super solution is to change check and print. 'print' will display the solutions in the entire N * N chessboard. Check(n) will check whether queen at row n is attacking any queen from row 0 to n-1.

Download the program from here :-
http://rapidshare.com/files/151974397/Nqueen.cpp.html

The ourput when NUMBER is 4 is as shown :-

x  Q  x  x
x  x  x  Q
Q  x  x  x
x  x  Q  x

x  x  Q  x
Q  x  x  x
x  x  x  Q
x  Q  x  x

Number of solutions 2

permutaions of the string

Following is the program for printing all the permutations of the given string using same technique. The changes are in print, check and the use of a new String tempStr. Str is the input and tempStr is the string which is used to for recursion. Instead of using ABCD, tempStr consists of characters '0','1','2',..etc. This only for program understading. If '0' is replaced by 'A' in the given program behavior will not change.
So for e.g. tempStr will take values like 0123 and 2301 instead of ABCD and CDAB.

The comments in the program will help to understand the program.

http://rapidshare.com/files/151640585/perm_string.cpp.html

The output of the given program will be

EFGH EFHG EGFH EGHF EHFG EHGF FEGH FEHG
FGEH FGHE FHEG FHGE GEFH GEHF GFEH GFHE
GHEF GHFE HEFG HEGF HFEG HFGE HGEF HGFE
Number of solutions 24

All subsets of a given set

Now using our recursive solution we will try to get all the subsets of a given set.
In following program Arrset is given set of integers and the program will print all the subsets. Each subset is shown using curly braces and commas separating elements{}. The function check is not needed in this case. The value of choice is two because for each element in the set we just have to check whether the element should be included in that particular subset or not. And finally the function print changes. Print will now check the value of element i and will print it as a part of subset or ignore it.
Instead of writing the program here, this time I have posted the program on Rapidshare, and giving the link.

http://rapidshare.com/files/151374580/rec_substring.cpp.html

The above program will produce the following output.

{} {8 } {7 } {7 8 } {6 } {6 8 } {6 7 } {6 7 8 }
{5 } {5 8 } {5 7 } {5 7 8 } {5 6 } {5 6 8 } {5 6 7 }
{5 6 7 8 }
Number of solutions 16

Super solution for exponential problems

This time I am proposing a super solution for all problems of exponential nature. Just by changing few parameters in this simple program can be used to find solutions for following problems and many other :-

1) All permutations and combinations problems
2) All permutations of the given string
3) Finding all the subsets of the given set
4) N-queen problem
5) Dynamic algorithm

/*This program is copyrighted by Manoj Ransing.
Use only for academic purpose*/

/*This program will print all the strings of length 3, 
where each one of the character can take value from
'0' to '3' e.g 000, 001, 002, 003, 010, 011, ..., 
300,..,333*/

#include <iostream>
using namespace std;

const char size = 3;/*This is the size of the elements*/
const char choice = 4;/*This is the number of choices for elements*/
string str(size,'0');/*The set of elements*/
long solutions = 0;/*Total number of solutions*/

/*Condition to continue recursing*/
bool check(int i)
{
return true;
};

/*Printing the solution*/
void print()
{
printf("%s ",str.c_str());
};

void perm(int n)
{
     /*This condition means end of the boundary,
     This must be one of the solution or output*/
     if(n == size)
     {
             solutions++;
             print();
             return;
     };
     /*This loop continues bounding values to elements*/
     for(int i=0; i<choice;i++)
     {
             str.at(n) = '0' + i;

             /*Check for the condition for the current element
             if condition satisfies recurse for the next n*/

             if(check(n))
                     perm(n+1);
     }
}

int main()
{
     perm(0);
     printf("\n");
     printf("number of solutions is %ld\n", solutions);
     return 0;
}

Output of the Above program is

000 001 002 003 010 011 012 013 
020 021 022 023 030 031 032 033 
100 101 102 103 110 111 112 113 
120 121 122 123 130 131 132 133 
200 201 202 203 210 211 212 213 
220 221 222 223 230 231 232 233 
300 301 302 303 310 311 312 313 
320 321 322 323 330 331 332 333
number of solutions is 64

I will put some more sample programs which uses this simple program to solve some known problems.

All subsets of a given set problem

This is a simple C program to print all the subsets of a given set. There will be (2ⁿ) subsets for a given set with n elements.

int main(void)
{
int set[] = {1,2,3,4,5,6,7,8};
const int setsize = sizeof(set) / sizeof (*set);

for (long i = (1 << setsize) -1; i >0 ; --i)

{
int index = setsize - 1;
int n = i;
cout<<'{';
while (n > 0)
{
       if (n % 2)
{
printf(" %d ", set[index]);
}
--index;
n /= 2;
}
cout<<'}'<<" ";
}
return 0;
}

set is the array of integers for which we need all subsets.
setsize is the number of elements in the set.
The for loop simply covers all the subsets, hence it executes (2ⁿ) times.
It uses a simple way to calculate subset. Assume the subset index i to be a binary number. Then it will print the element j from the set, if in i j is set. e.g. if i = 23.
i = 16 + 4 + 2 + 1 = 2⁴ + 2² + 2¹+2⁰.
Hence for i=23, the program will simply print 4th, 2nd, 1st and 0th indexed element from set.

Just give some time with the program and you will easily undestand how it works.

Currently I am trying to do the same thing using recursion and without using any extra space. The obvious solution is at any step adding current element to all the subsets created before that step. But this will surely take 2ⁿ space.